こんにちはAkiraです。
本日の学習時間は5時間でした。
今日も勉強が捗りました。
学習の進捗
本日は速修テキスト(経済学、経済政策)の第6章、第7章のインプットを行いました。
学習内容
- 消費者行動理論
- 生産者行動理論
ついにミクロ経済の分野スタートです。
マクロ経済ではIS曲線とLM曲線の理解に苦しみましたが、
ミクロ経済でも理解に苦しむ箇所が出てきました。
それは需要の価格弾力性の項に書かれている、「需要曲線が直線の場合、需要曲線の中心の価格と数量の組み合わせのとき、需要の価格弾力性は1となる」という部分です。
テキストと講義動画ではさらっと進んでしまった部分でした。
正直この部分については深追いせず、この文章をそのまま暗記しようかなと思ったんですが、
休日ということもあり、自分なりに考えてみました。
需要の価格弾力性について
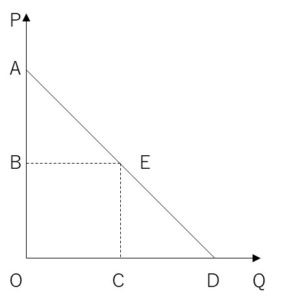
まずは講義動画の中にあった、需要の価格弾力性=BO/AB=CD/OCという式をもとめてみたいと思います。
需要の価格弾力性は、その名前の通りその財の価格の変化率に対する需要の変化率の割合のことですので、
需要の価格弾力性 = (ΔQ/Q)/(ΔP/P)
というのが需要の価格弾力性の定義になります。
Qが需要、Pが価格を表します。
ここでこの式を変形すると、
需要の価格弾力性= (ΔQ/ΔP)・(P/Q) …①
となります。
需要曲線が直線という前提ですので、上の図で点Aから点Eまで需要が変化した場合を考えると、
ΔP=AB …②
ΔQ=BE …③
P=OB (点Eでの価格) …④
Q=OC (点Eでの需要) …⑤
となります。(点Eでの価格をOBといったように、図形的に原点からの距離で表しています。)
上記の②~⑤を①の式に代入すると
需要の価格弾力性=(BE/AB)・(OB/OC) …⑥
となり、図形的にBE=OCですから、⑥の式に代入すると
需要の価格弾力性=(OC/AB)・(OB/OC) =OB/AB
となります。
同様に上の図で需要が点Eから点Dまで変化した時を考えると、
需要の価格弾力性=CD/OC
が導き出せます。
そのため需要曲線(この場合は直線ですが)の中点ではOB=ABとなり、価格弾力性が1となるんですね。
