自作キーボードのDuplex Matrixとはなにか調べてみた

とあるYouTube動画最近を見て、Keyballという今話題のトラックボール内蔵の自作キーボードに非常に興味を持ちました。
白金ラボさんが設計・開発・販売されている自作キーボードキットになります。
Keyballはキー数の違いによりいくつかのバージョンがあるのですが、最もキー数の多いKeyball61では、61個のキースイッチとトラックボールの両方を認識するために、Duplex Matrixを使用しているとのこと。
初めてDuplex Matrixというものを聞いたので、Duplex Matrixについて調べてみました。

通常のマトリクススキャン

自作キーボードでは、キー(キースイッチ)は縦方向と横方向のマトリクス状に接続されています。
小さい例を挙げると、2×2のキーボードは下記の図のような回路図で繋がっています。

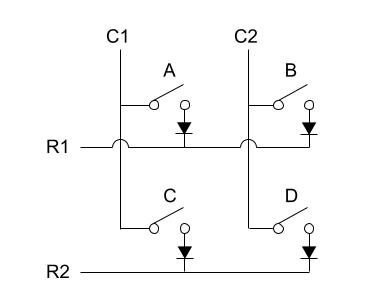
COL2ROW

縦方向で見ると、キーAとキーCはC1(Col1)につながり、キーBとキーDはC2(Clo2)につながっています。
横方向で見ると、キーAとキーBはR1(Row1)につながり、キーCとキーDはR2(Row2)につながっています。
キー１つに対し、ダイオードが接続されていますが、なぜこのダイオードが必要なのかは、下記の記事を参照してください。

どのキーが押されているかを判定するために、Pro Micro内に書かれたプログラムは列方向の端子の電圧を順番にHigh(=5V)にしていきます。
上の2×2のマトリクスではまずC1をHighにし、次にC2をHighにし、またC1をHighにするということを繰り返し実施します。
そして、それぞれの列方向の端子をHighにしたときに、どの行方向の端子がHighになったかを見て、どのキーが押されたかを判別します。
例えば下の図のように、キーBを押した場合、C2をHighにしたときに、赤い矢印のように回路が繋がるので、R1の端子がHighになります。
つまり、C2をHighにしたときにR1がHighになればキーBが押されていると、判定できるわけです。
このように列方向の端子を順番にHighにしていき、行方向の端子の電圧を見ることを、マトリクススキャンと呼ぶようです。

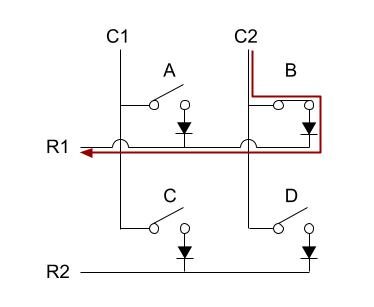
COL2ROW_example

上の図の例では列から行へ電流が流れる方法で説明しました。
これはCOL2ROWと呼ばれる方向です。
これとは逆に行から列へ電流が流れる方法でもマトリクススキャンを行えます。
この向きはROW2COLと呼ばれています。
例えば下の図のようにダイオードを逆向きに接続することで、行方向から列方向へのスキャンが可能になります。
この場合R1の端子をHighにし、次にR2の端子をHighにし、またR1の端子をHighにするということを繰り返していきます。

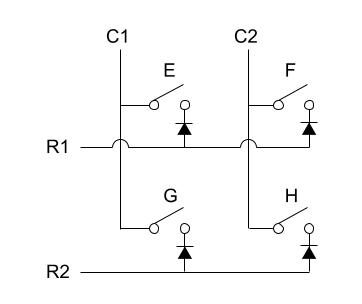
ROW2COL

例えば、下の図のようにキーHを押した場合、赤い矢印のように回路がつながるため、R2をHighにしたとき、C2がHighになります。
Pro Micro内のプログラムはR2をHighにしたときにC2がHighになれば、キーHが押されていると認識します。

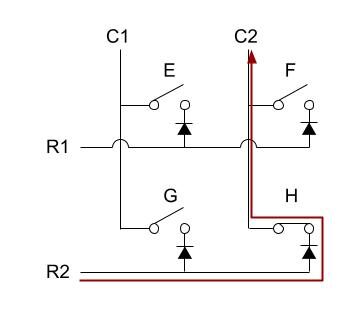
ROW2COL_example

Duplex matrixでのマトリクススキャン

Duplex matrixでは、上記で紹介したCOL2ROWとROW2COLの両方のマトリクススキャンを実施します。
これまでの例と同じように列方向、行方向ともに2つずつ端子がある場合のDuplex matrixでの回路図は下記のようになります。
これまでに紹介したCOL2ROWとROW2COLの両方を並べたような回路になります。
これまでとの違いは、C1→C2と列方向の端子をHighにして、どの行方向の端子がHighになるかみた後、
今度はR1→R2の行方向の端子をHighにして、どの列方向の端子がHighになるかとみることです。
つまり列から行へのスキャンと、行から列へのスキャンを順番に繰り返し行なっています。
こうすることで、端子はこれまで通り4つ(列方向2端子+行法今日2端子)ですが、認識できるキーの数は8個と倍になっています。

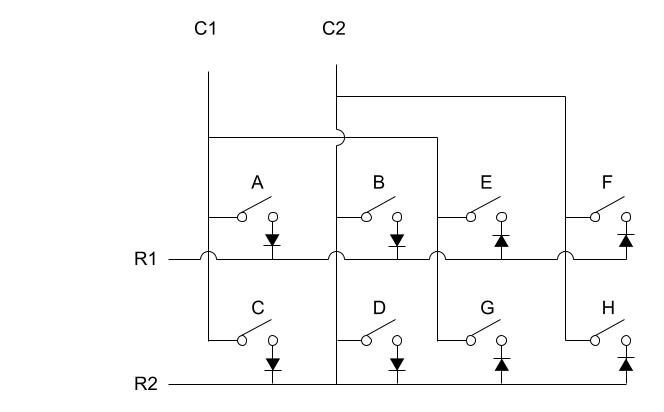
Duplex_matrix

下の図は、どのようにキーが認識されているかを示しています。
例えばBのキーが押された場合は、赤い矢印の回路がつながるので、C2をHighにしたときにR1がHighになることで認識されます。
この時、例えばHのキーを押したとしても、Hのキーにつながっているダイオードが行方向から列方向であるため、R2がHighになることはありません。
Hのキーが押されたと認識できるのは、青い矢印のようにR2をHighにしてC2がHighになる行方向から列方向へのスキャンの時です。
このようにダイオードの向きを変えたマトリクスを配置し、列方向から行方向へのスキャンと、行方向から列方向へのスキャンを繰り返すことで、同じ端子数でも倍のキー数を認識できるのがDuplex matrixです。

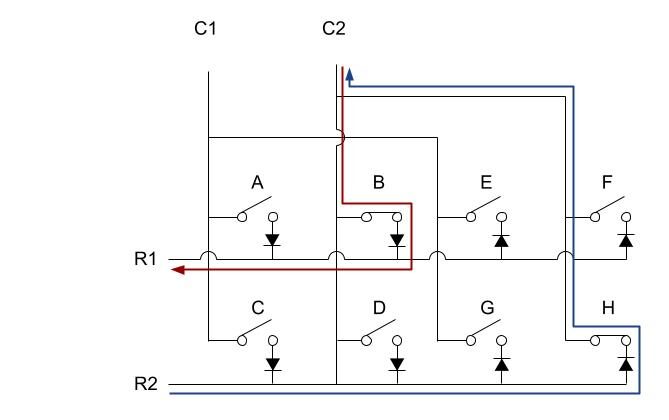
Duplex_matrix_example

最後に

いかがでしたでしょうか？
私は、このような自作キーボードの仕組みを理解することで、どんどん自作キーボードの沼に嵌っていっております。